第一节 比色分析的基本原理
比色分析是基于溶液对光的选择性吸收而建立起来的一种分析方法,又称吸光亮度法。
有色物质溶液的颜色与其浓度有关。溶液的浓度越大,颜色越深。利用光学比较溶液颜色的深度,可以测定溶液的浓度。
根据吸收光的波长范围不同以及所使用的仪器精密程度,可分为光电比色法和分光亮度法等。
比色分析具有简单、快速、灵敏度高等特点,广泛应用于微量组分的测定。通常中测定含量在10-1~10-4mg·L-1的痕量组分。比色分析如同其他仪器分析一样,也具有相对误差较大(一般为1%~5%)的缺点。但对于微量组分测定来说,由于绝对误差很小,测定结果也是令人满意的。在现代仪器分析中,有60%左右采用或部分采用了这种分析方法。在医学学科中,比色分析也被广泛应用于药物分析、卫生分析、生化分析等方面。
一、物质的颜色和光的关系
光是一种电磁波。自然是由不同波长(400~700nm)的电磁波按一定比例组成的混合光,通过棱镜可分解成红、橙、黄、绿、青、蓝、紫等各种颜色相连续的可见光谱。如把两种光以适当比例混合而产生白光感觉时,则这两种光的颜色互为补色。图8-1中处于同一直线关系的两种色光(如绿与紫、黄与蓝)互为补色。
当白光通过溶液时,如果溶液对各种波长的光都不吸收,溶液就没有颜色。如果溶液吸收了其中一部分波长的光,则溶液就蜈现透过溶液后剩余部分光的颜色。例如,我们看到KMnO4溶液在白光下呈紫红色,就是因为白光透过溶液时,绿色光大部分被吸收,而其他各色都能透过。在透过的光中除紫红色外都能两两互补成白色,所以KMnO4溶液呈现紫红色。
同理,CuSO4溶液能吸收黄色光,所以溶液呈蓝色。由此可见,有色溶液的颜色是被吸收光颜色的补色。吸收越多,则补色的颜色越深。比较溶液颜色的深度,实质上就是比较溶液对它所吸收光的吸收程度。表8-1列出了溶液的颜色与吸收光颜色的关系。
表8-1 溶液的颜色与吸收光颜色的关系
| 溶液颜色 | 绿 | 黄 | 橙 | 红 | 紫红 | 紫 | 蓝 | 青蓝 | 青 | |
| 吸收光 | 颜色 | 紫 | 蓝 | 青蓝 | 青 | 青绿 | 绿 | 黄 | 橙 | 红 |
| 波长/nm | 400~450 | 450~480 | 480~490 | 490~500 | 500~560 | 560~580 | 580~600 | 600~650 | 650~760 | |
二、朗伯-比尔(Lambert-Beer)定律
当一束平行单色光(只有一种波长的光)照射有色溶液时,光的一部分被吸收,一部分透过溶液(图8-2)。
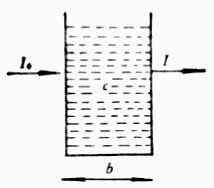
图8-2 光吸收示意图
设入射光的强度为I0,溶液的浓度为c,液层的厚度为b,透射光强度为I,则
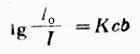
(8-1)
式中lgI0/i 表示光线透过溶液时被吸收的程度,一般称为吸亮度(A)或消亮度(E)。因此,上式又可写为:
A=Kcb(8-2)
上式为朗伯-比尔定律的数学表示式。它表示一束单色光通过溶液时,溶液的吸光度与溶液的浓度和液层厚度的乘积成正比。
式中,K为吸光系数,当溶液浓度c和液层厚度b的数值均为1时,A=K,即吸光系数在数值上等于c和b均为1时溶液的吸光度。对于同一物质和一定波长的入射光而言,它是一个常数。
比色法中常把
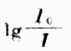
称为透光度,用T表示,透光度和吸光度的关
系如下:
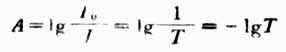
(8-3)
当c以mol·L-1为单位时,吸光系数称为摩尔吸光系数,用ε表示,其单位是L·mol-1·cm-1。当c以质量体积浓度(g·ml-1)表示时,吸光系数称为百分吸光系数,用E1%1cm表示,单位是ml·g-1·cm-1。吸光系数越大,表示溶液对入射光越容易吸收,当c有微小变化时就可使A有较大的改变,故测定的灵敏度较高。一般ε值在103以上即可进行比色分析。
如果测定某种物质对不同波长单色光的吸收程度,以波长为横坐标,吸光度为纵坐标作图可得一条曲线,即物质对光的吸收曲线,可准确地描述物质对光的吸收情况。
图8-3是几种不同浓度的KMnO4溶液的吸收曲线,溶液对波长525nm附近的绿光吸收量最强,而对其他波长的光吸收较弱。光吸收程度最大处的波长叫做吸收波长,用λmax表示。不同浓度的KMnO4溶液所得的吸收曲线,最大吸收波长都一致,只是相应的光被吸收的程度不同。
吸收曲线可作为比色分析中波长选定的依据,测定时一般选择λmax 的单色光作为入射光。这样即使被测物质含量较低也可得到较大的吸光度,因而可使分析的灵每度较高。
若所测定的溶液无色,可在测定前加入适当的显色剂,通过与待测成分的化学反应使溶液晱色即可测定此待测成分。
例如, 已知在525nm处KnO4溶液的ε=2235L· mol-1·cm-1,若用2cm比色皿,为使所测得的透光率介于20%~65%之间,溶液的浓度范围应是多少?
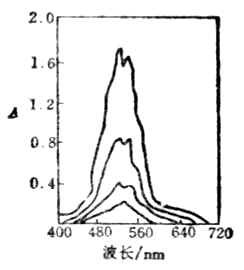
图8-3 KMnO4液的吸收光谱曲线
解:若T=20%
则
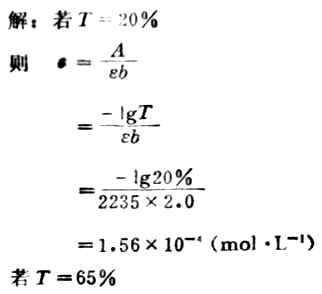
则 c=-lg65%/2235*2.0=4.19*10-5(mol·L-1)
